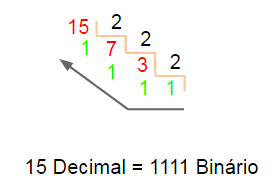
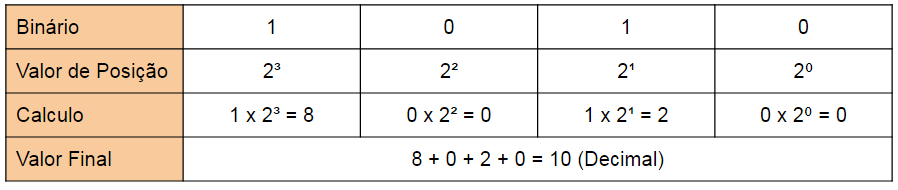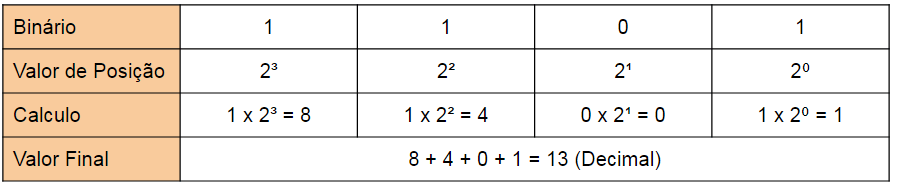“Existem 10 tipos de pessoas no mundo,
quem entende de números binários e quem não.”
Um número binário é composto de apenas 0 e 1. Por exemplo;
110100
Na computação, o binário representa o estado de uma corrente elétrica, que pode estar desligada ou ligada, ou seja, pode estar no estado 0 ou 1. Através de várias combinações de correntes elétricas ligadas e desligadas o computador é capaz de criar cálculos e tomar decisões.
Não há 2, 3, 4, 5, 6, 7, 8 ou 9 no binário!
Entendemos que a base decimal são números formados por dígitos de 0 a 9, quando chegamos no 9 começamos a repetir os dígitos de modo que eles formem a menor combinação possível, eis que encontramos o 10, depois o 11 e assim por diante.
No binário o raciocínio é o mesmo, começamos com a sequência de 0 e 1 e depois do 1 começamos a combinar os dígitos de modo a formar a menor combinação possível, eis que encontramos o 10, depois o 11, 100, 101 e assim por diante.
A tabela abaixo mostra a sequência de números decimais com seus respectivos valores em Binário.
| Dec10 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Bin2 | 0 | 1 | 10 | 11 | 100 | 101 | 110 | 111 | 1000 | 1001 | 1010 |
Conversão de binário para decimal
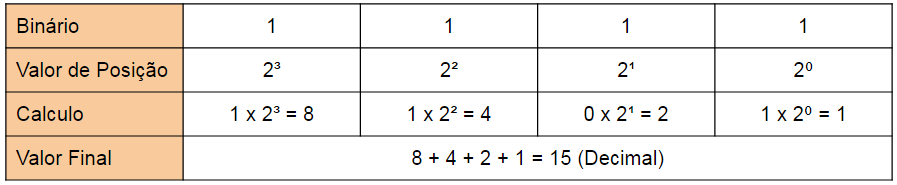
Exemplo: Qual o valor de 11112 em decimal?
- O “1” à esquerda está na posição “2 × 2 × 2”, o que significa 1 × 2 × 2 × 2 (= 8)
- O próximo “1” está na posição “2 × 2”, o que significa 1 × 2 × 2 (= 4)
- O próximo “1” está na posição “2”, o que significa 1 × 2 (= 2)
- O último “1” está na posição uns, o que significa 1
- Resposta: 1111 = 8 + 4 + 2 + 1 = 15 em decimal
Exemplo: Qual o valor de 10012 em decimal?
- O “1” à esquerda está na posição “2 × 2 × 2”, o que significa 1 × 2 × 2 × 2 (= 8)
- O “0” está na posição “2 × 2”, o que significa 0 × 2 × 2 (= 0)
- O próximo “0” está na posição “2”, o que significa 0 × 2 (= 0)
- O último “1” está na posição uns, o que significa 1
- Resposta: 1001 = 8 + 0 + 0 + 1 = 9 em decimal
Exemplo: Qual o valor de 1,12 em decimal?
- O “1” no lado esquerdo está na posição uns, o que significa 1.
- O 1 no lado direito está na posição “metades”, o que significa 1 × (1/2)
- Portanto, 1,1 é “1 e 1 meio” = 1,5 no decimal
Exemplo: Qual o valor de 10,112 em decimal?
- O “1” está na posição “2”, o que significa 1 × 2 (= 2)
- O “0” está na posição uns, o que significa 0
- O “1” à direita do ponto está na posição “metades”, o que significa 1 × (1/2)
- O último “1” no lado direito está na posição “quartos”, o que significa 1 × (1/4)
- Assim, 10,11 é 2 + 0 + 1/2 + 1/4 = 2,75 em decimal
Conversão do sistema decimal para binário
